miércoles, 30 de abril de 2014
martes, 29 de abril de 2014
4 PROBLEMAS INTERESANTES
1) Resuelva el amable lector el siguiente criptograma. Cada ? representa un símbolo que debe encontrarse.
SOLUCIÓN
¿Puede calcularlo el amable lector?. Tome la densidad del terreno igual a 2000 kg/m³ y recuerde que el radio de la tierra es 6730 km, y su masa, 6*1024 kg.
El peso de un cuerpo en la superficie terrestre es la composición de las atracciones sobre él de todos los átomos de la Tierra, y equivale a la que ejercería la masa de ésta concentrada en su centro. El hueco de la excavación supone introducir en ese conjunto una asimetría substractiva, cuyo resultado neto es lógicamente una repulsión del mismo valor que la atracción gravitatoria que ejercería el volumen de tierras del hueco.
Se puede asimilar también ésta, bastante aproximadamente, a la que ejercería una masa equivalente contentrada en el centro de gravedad de la excavación, o sea:Donde las respectivas masa y distancia de acción valen:El cociente entre ambas fuerzas vale:Este es el ángulo que se desviará la plomada de la vertical. En una distancia de 12 metros, equivale a:Esta desviación es ciertamente inapreciable, pero no lo sería tanto en el caso de una gran excavación, como las de algunas explotacoines metalúrgicas a cielo abierto en Chile o Sudáfrica, en que algunas de las dimensiones anteriores pueden ser de kilómetros. Para un hueco de 500*500*120 m, la desviación de la plomada en el fondo sería de ¡0,7 mm!, claramente perceptible.
4)
| M | I | L | |||||
| + | M | I | L | ||||
| _ | _ | _ | _ | _ | _ | _ | _ |
| ? | ? | ? | ? | ? | ? | ? |
Los símbolos son: M M X C V I I I .
La suma está expresada en numeración romana. Así:
Entre los bloqueos conceptuales se encuentra el de falso hecho admitido, por ello para la resolución de problemas no hay nunca que dar por sentado más que lo que específicamente se exprese en el enunciado. En este caso, admitir sin más, que los símbolos expresan dígitos, cierra el camino hacia la solución.
La suma está expresada en numeración romana. Así:
| M | I | L | 1 | 0 | 4 | 9 | ||||||||||||||
| + | M | I | L | + | 1 | 0 | 4 | 9 | ||||||||||||
| _ | _ | _ | _ | _ | _ | _ | _ | _ | _ | _ | _ | _ | ||||||||
| M | M | X | C | V | I | I | I | 2 | 0 | 9 | 8 |
Entre los bloqueos conceptuales se encuentra el de falso hecho admitido, por ello para la resolución de problemas no hay nunca que dar por sentado más que lo que específicamente se exprese en el enunciado. En este caso, admitir sin más, que los símbolos expresan dígitos, cierra el camino hacia la solución.
2) Determinar la probabilidad de que en un sorteo de Lotería Primitiva aparezcan al menos dos números consecutivos cualesquiera.
SOLUCIÓN
La solución más sencilla pasa por calcular el número de combinaciones en las que no hay números consecutivos y restarlo luego del total.
Consideremos los dos conjuntos siguientes:
C1 = Combinaciones de 6 números del 1 al 49 tales que entre ellos no hay dos consecutivos.
C2 = Combinaciones cualesquiera de números del 1 al 44.
Ambos conjuntos tienen igual número de elementos, dado que existe entre ellos la siguiente correspondencia biunívoca: (a,b,c,d,e,f) <-> (a,b-1,c-2,d-3,e-4,f-5)
dónde a,b,c,d,e,f son números entre 1 y 49 tales que no hay entre ellos dos consecutivos. Por ejemplo, la combinación (1,5,7,20,35,49) de C1 se correspondería con la (1,4,5,17,31,44) de C2. El número de C2 es el combinacional de 44 sobre 6 = 7.059.052. Puesto que C1 y C2 tienen el mismo número de elementos Card(C1)=Card(C2)=7.059.052.
La cantidad total de combinaciones de la Lotería Primitiva es el combinacional de 49 sobre 6 = 13.983.816.
Luego, el número de tales combinaciones en las que no hay dos elementos consecutivos es la diferencia: 13.983.816 - 7.059.052 = 6.924.764
La probabilidad de que salgan dos números consecutivos cualesquiera en un sorteo es, en consecuencia 49,52%.
Consideremos los dos conjuntos siguientes:
C1 = Combinaciones de 6 números del 1 al 49 tales que entre ellos no hay dos consecutivos.
C2 = Combinaciones cualesquiera de números del 1 al 44.
Ambos conjuntos tienen igual número de elementos, dado que existe entre ellos la siguiente correspondencia biunívoca: (a,b,c,d,e,f) <-> (a,b-1,c-2,d-3,e-4,f-5)
dónde a,b,c,d,e,f son números entre 1 y 49 tales que no hay entre ellos dos consecutivos. Por ejemplo, la combinación (1,5,7,20,35,49) de C1 se correspondería con la (1,4,5,17,31,44) de C2. El número de C2 es el combinacional de 44 sobre 6 = 7.059.052. Puesto que C1 y C2 tienen el mismo número de elementos Card(C1)=Card(C2)=7.059.052.
La cantidad total de combinaciones de la Lotería Primitiva es el combinacional de 49 sobre 6 = 13.983.816.
Luego, el número de tales combinaciones en las que no hay dos elementos consecutivos es la diferencia: 13.983.816 - 7.059.052 = 6.924.764
La probabilidad de que salgan dos números consecutivos cualesquiera en un sorteo es, en consecuencia 49,52%.
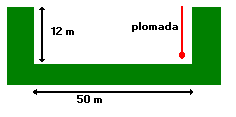
3) Mi empresa ejecuta una obra, de la que se ha completado la excavación. Esta consiste, aproximadamente, en un vaciado de planta cuadrada, con 50 m de lado y 12 m de profundidad. Conversando un día con un arquitecto compañero, se nos ocurrió si la plomada librada a lo largo de uno de los lados de la excavación se desviaría mucho de la vertical como consecuencia del vaciado.
¿Puede calcularlo el amable lector?. Tome la densidad del terreno igual a 2000 kg/m³ y recuerde que el radio de la tierra es 6730 km, y su masa, 6*1024 kg.

SOLUCIÓN
La aceleración de la gravedad g vale 9,81 m/s².
g = GM/R² = 9.81 m/s²siendo G la constante de gravitación universal, M la masa de la Tierra y R su radio.
El peso de un cuerpo en la superficie terrestre es la composición de las atracciones sobre él de todos los átomos de la Tierra, y equivale a la que ejercería la masa de ésta concentrada en su centro. El hueco de la excavación supone introducir en ese conjunto una asimetría substractiva, cuyo resultado neto es lógicamente una repulsión del mismo valor que la atracción gravitatoria que ejercería el volumen de tierras del hueco.
Se puede asimilar también ésta, bastante aproximadamente, a la que ejercería una masa equivalente contentrada en el centro de gravedad de la excavación, o sea:
g' = Gm'/r'²
m' = 50.50.12.2000 = 6.107 kg r' = (25² + 6²)½ = 25,71 m
g' 6.107.(6,37.106)² - = ------------------- g 6.1024.(25,71)² g'/g = 6,14*10-7
La componente horizontal de esa fuerza vale:
g'x /g = 6,14.10-7 (25/25,71) = 5,97 .10-7
x = 12.5,97.10-7 m = 7,16.10-6 m = 0,00716 mm
2x - 3y = 1
SOLUCIÓN
Puesto que la diferencia es positiva se cumple que x > y. Procediendo al cambio de variable x = a+y la expresión queda:2a+y - 3y = 1 => 2a 2y - 3y = 1 => 2a(10/5)y - 3y = 1 => 2 a 10 y = 15 y + 5 y (I)El primer miembro de (I) termina en "y" ceros. Vamos a ver en cuantos ceros termina el segundo miembro. Obtenemos las primeras potencias de 15 y 5. Si nos fijamos en las terminaciones vemos que:
y 15y 5y La suma 15y + 5y termina en "y" ceros 0 1 1 0 1 5 5 1 2 225 25 1 3 3375 125 2 4 50625 625 1 5 759375 3125 2
Cuando y>2 15ytermina 5ytermina La suma termina Impar 375 125 500 (2 ceros) Par 625 625 350 (1 cero) Es así porque 375 x 15 termina en 625 y 125 x 5 termina en 625 mientras que 625 x 15 termina en 375 y 625 x 5 en 125Luego la igualdad (I) no se cumple para y>2: Primer miembro 2 ceros, segundo miembro 1 cero (225+25=250). Como consecuencia, la ecuación planteada sólo puede cumplirse para y<=2, concretamente para (1,0) y (2,1).
TOMADO DE: http://www.mensa.es/juegosmensa/e001005.html#ENUN001
lunes, 28 de abril de 2014
domingo, 27 de abril de 2014
Problemas San Gaku o Problemas Bonitos de GeometrÍa resueltos por Métodos Elementales
sábado, 26 de abril de 2014
ILUSIONES ÓPTICAS
Vaquero joven o viejo.

Joven saxofonista.

Esquimal o indio.

TOMADOS DE: http://www.juegosdelogica.com/neuronas/ilusiones.htm
QUÉ OBSERVAS? ( UN NIÑO)

RANA O CABALLO?
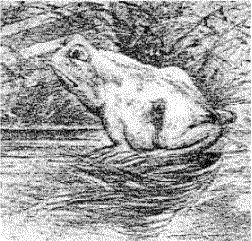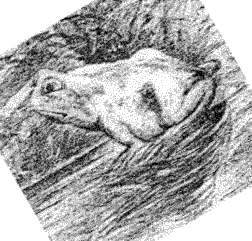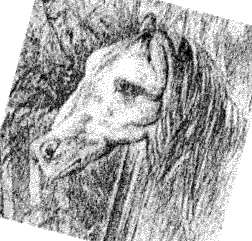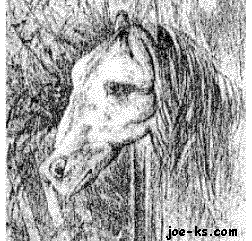
TOMADO DE: https://josmapell.wordpress.com/category/ilusiones-opticas/
viernes, 25 de abril de 2014
CURIOSIDADES MATEMÁTICAS 4
NUMEROLOGIA CARROLLIANA: EL 55
● El décimo triangular (55 = 1 + 2 + 3 + … + 10). Con el 66 y el 666 son los únicos números de
menos de 30 dígitos que son triangulares y formados por un solo dígito repetido.
● Es también el quinto número piramidal cuadrado, es decir, el correspondiente a esferas
apiladas formado una pirámide de base cuadrada. La fórmula general para estos números es Pn
= n(n+1)(2n+1)/6. O, lo que es lo mismo, es el quinto holopotencial de segundo orden:
2 2 2 2 2
55 = 1 + 2 + 3 + 4 + 5.
● El décimo en la serie de Fibonacci (un = un-1 + un-2; ui
= { 1, 1, 2, 3, 5, 8, 13, 21, 34, 55…} ).
Los únicos números que son a la vez triangulares y de Fibonacci son el 1, el 3, el 21 y el 55.
● Es el tercer decatópico (suma de los tres primeros eneatópicos). Tras los números triangulares
vienen los tetraédricos (suma de los n primeros triangulares), tetratópicos (suma de los n
primeros tetraédricos)… y decatópìcos, suma de los primeros eneatópicos. Su fórmula general
es:
n+8
Dn = ( )
...9
● Es el cuarto número de Kaprekar. Son números de Kaprekar los que una vez elevados al
cuadrado, la suma de la mitad izquierda y la derecha de éste reproducen el número (v. gr., 297,
2
pues 297 = 88209, y 88 + 209 = 297. Los primeros números de Kaprekar son 1, 9, 45, 55,
297, 703…
● Es un cúbico con recurrencia digital invariante. Es decir:
3 3
5 + 5 = 250
3 3 3
2 + 5 + 0 = 133
3 3 3
1 + 3 + 3 = 55
Cualquier número mayor de 55 es la suma de primos distintos de la forma 4n + 3.
● Es uno de los protagonistas de la siguiente curiosidad aritmética:
2 2
8 - 3 = 5 8 - 3 = 55
2 2
78 - 23 = 55 78 - 23 = 555
2 2
778 - 223 = 555 778 - 223 = 5555
2 2
7778 - 2223 = 5555 7778 - 2223 = 55555
TOMADO DE:http://www.mensa.es/carrollia/c55.pdf
La magia de llegar a la tabla del 12
La magia de llegar a la tabla del 12
Rob Eastaway
Autor y matemático, especial para la BBC
Domingo, 28 de julio de 2013
Ir más allá de la tabla del 10 también tiene algo de juego.
No se trata de aprender a memorizar, sino de disfrutar de la profusión de patrones que se revelan cuando aprendemos a multiplicar, asegura el escritor y matemático Rob Eastaway.
Hubo una época, hace varias décadas, en la que muchos niños del mundo tenían una razón obvia para aprenderse la tabla del 12. Todos los países que usaban las medidas imperiales británicas calculaban en pies y pulgadas y pagaban en chelines y peniques.
Multiplicar por 12 era una experiencia cotidiana.
Pero eso es historia antigua, aunque los huevos aún se venden en docenas, y mucha gente -incluidos los estadounidenses- todavía midan en pulgadas.
Nada de eso justifica pasar horas repitiendo esas tablas extra.
Y sin embargo, sigue habiendo una razón para aprenderse "la del doce". Algo que tiene más que ver con el descubrimiento de patrones y con tener confianza al manejar números.
Apenas los niños se empiezan a sentir cómodos multiplicando números más grandes que 10, comienzan a entender las multiplicaciones largas.
Saberse las tablas del 11 y del 12 puede introducir patrones intrigantes de los que podrían perderse si paran en la del 10.
Lo divertido del 11
Mucho de la tabla de multiplicar por 11 es fácil de aprender: 2 x 11 es 22, 8 veces 11 es 88. Y cuando uno pasa de 12, hay patrones simpáticos para descubrir.
¿Quiere multiplicar 11 x 23? Simplemente tome los dos dígitos -2 y 3-, súmelos (da 5) y ponga ese número en la mitad: 253. ¡Tadaaaa!
¿Qué tal 36 x 11? De nuevo, separe el 3 del 6 y ponga su suma en la mitad: 396. Maravilloso.
¡Pero cuidado! Si los dos dígitos suman más de 9, este genial truco no funciona tan bien.
58 x 11... pues 5 + 8 = 13, pero la respuesta no es 5138. Ese "1" del 13 realmente representa a un 10, por lo que tiene que ser añadido al 5 para que dé la respuesta correcta: 638.
Hay otro patrón que empieza con 11 x 11.
Multiplique esos dos número y le da 121.
¿Y 111 x 111? La respuesta es 12321.
¿Puede adivinar cuánto es 1111 x 1111? 1234321.
El 12
Multiplicar por 12, por su lado, es más simple cuando uno se da cuenta de que es lo mismo que multiplicar un número por 10 y añadir el doble del primer número.
Entonces, 12 x 12 es 10 x 12 (=120), y luego se le añade 2 x 12 (=24), lo que da 120 + 24 = 144.
Esa regla no se limita a la tabla de multiplicar, que se suspendería en 12 x 12.
12 x 61 es lo mismo que 10 x 61 (=610) más 2 x 61 (=122) y si puede sumar 610 + 122 en su mente, tendrá la respuesta correcta: 732.
¿Es necesario memorizar la respuesta de 12 x 12? Realmente no. Mientras se acuerde de la estrategia para hacer los cálculos, llegará a la respuesta con casi la misma rapidez.
Pero claro, al hacerlo a menudo, se queda en la memoria, lo que agiliza el proceso en esos momentos en los que necesita un resultado pronto.
¿Seguir hasta 20?
¿Por qué parar en la tabla del 12? Se podría seguir con la del 13, 14... hasta la del 20, como se hace en algunos países.
Lo que pasa es que si uno entiende las tablas de multiplicar básicas hasta el 10, tiene las herramientas necesarias para llegar al resultado de, digamos, 19 x 14.
Y si uno pasa demasiado tiempo memorizando las respuestas a esas preguntas, no va a tener tiempo para entender cómo funcionan los números.
De lo que realmente se tratan las matemáticas es de entender patrones y resolver problemas.
Rob Eastaway es coautor del libro "Mateméticas para mamás y papás".
TOMADO DE:http://www.bbc.co.uk/mundo/noticias/2013/07/130705_tablas_multiplicar_defensa_finde.shtml
jueves, 24 de abril de 2014
CURIOSIDADES MATEMÁTICAS 3
¿Qué pasaría si...





.quisiéramos calcular la longitud de la “hipotenusa” en este “triángulo” rectángulo?
 |
¿Qué fórmula obtendríamos?
Respuesta: La longitud de la “hipotenusa” es igual a la suma de las longitudes de los otros dos lados. Aquí va la justificación.
Indiquemos las tres longitudes con a, b, c, como se ve en la Figura 1:

Independientemente de cómo construyamos los escalones que forman el “lado” c, la suma de las longitudes de todos los segmentos verticales debe ser igual a b; de la misma manera, las longitudes de todos los segmentos horizontales debe darnos a. ¡O sea que
c = a + b !
Observemos que esto no puede cumplirse en ningún triángulo rectángulo (Figura 2),

pues por una parte tendríamos a + b = c, mientras que el teorema de Pitágoras nos diría que
a2 + b2 = c2.
O sea,
a2 + b2 = a2 + 2ab + b2,
lo cual implicaría que 2ab = 0 ó que uno de los lados, a ó b, debe tener longitud cero. Es decir, que no tendríamos un verdadero triángulo.
Recordemos que lo que sí es verdad en cualquier triángulo, rectángulo o no, es que la longitud de cada lado no puede ser mayor que la suma de las longitudes de los otros dos lados. Es decir (Figura 3),
c ≤ a + b.

Podemos preguntarnos si habrá algún triángulo para el cual esta desigualdad se convertirá en una igualdad. La respuesta es que no, si queremos tener un verdadero triángulo. Efectivamente, el teorema del coseno (Figura 4) nos dice:
c2 = a2 + b2 – 2ab cos θ.

Si fuera c = a + b, tendríamos
a2 + 2ab + b2 = a2 + b2 – 2ab cos θ .
O sea,
ab = – ab cos θ .
Como las longitudes a y b son ambas mayores que cero debe ser cos θ = – 1, de donde resulta que el ángulo θ tiene que valer 180º. Es decir, que el triángulo tiene que reducirse a:

Figura 5.
Sobre la autora
| |
 |
Josefina (Lolina) Álvarez es Professor of Mathematics en New Mexico State University (USA). Especialista en análisis armónico y funcional, se doctoró en Matemáticas por la Universidad de Buenos Aires (Argentina)
TOMADO DE:
http://www.matematicalia.net/index.php?option=com_content&task=view&id=387&Itemid=234
|
miércoles, 23 de abril de 2014
Arcos con geometría dinámica (GeoGebra), I (*)
José Manuel Arranz, Rafael Losada, José Antonio Mora y Manuel Sada
Equipo G4D
página web: http://geometriadinamica.es
En este artículo se propone el diseño de diez de los arcos utilizados en arquitectura con el programa de geometría dinámica GeoGebra. Para cada uno de ellos se ha intentado disfrazar las instrucciones de construcción con una guía en forma de secuencia animada que quiere parecerse en cierto modo a las utilizadas en las construcciones de Lego: partiendo de las piezas iniciales, unas pocas ideas visuales nos van acercando en pequeños saltos al resultado final. El lector podrá utilizar los applets para construir el arco propuesto con todas las funcionalidades de GeoGebra en su navegador.
Se incluye, además, una propuesta de trabajo comentada para la clase y las soluciones aportadas por dos grupos de alumnos de secundaria de edades comprendidas entre 12 y 14 años, uno de ellos en el IES Sant Blai de Alicante y el otro formado por los participantes en el proyecto ESTALMAT de la Comunidad Valenciana.
1. Introducción
Arcos con geometría dinámica se enmarca en un trabajo más amplio en el que se exploran las relaciones entre geometría y arte, que se puede encontrar en el portal colectivo del grupo G4D [http://geometriadinamica.es]. Como equipo participamos en el Instituto GeoGebra de Cantabria [http://www.geogebra.org/IGI] y en el proyecto Intergeo de la Unión Europea [http://www.inter2geo.eu/es], entre cuyos objetivos se encuentra conseguir que los contenidos de geometría dinámica sean cada vez más accesibles, se utilicen con mayor frecuencia y se les pueda sacar mejor partido en la enseñanza de las matemáticas en Europa.
La idea de construir los arcos con geometría dinámica surgió de los trabajos de José Manuel Arranz, quien en su página web http://roble.pntic.mec.es/jarran2/cabriweb/arcos/arcos.htm incluye una gran colección de diseños. En ella, José Manuel nos presenta cada arco junto con la secuencia de trabajo para diseñarlo.
1.1 Aspectos técnicos de los arcos
Un arco es un elemento utilizado en arquitectura para unir dos pilares o dos muros con piezas pequeñas. De esta forma podemos construir una edificación sobre un hueco: una casa, un puente o un acueducto. Aquí tienes las imágenes de algunos arcos obtenidos de Wikipedia: el Arco del Triunfo en París, el Monasterio de las Huelgas en Burgos y La Pedrera en Barcelona, obra de Gaudí.
 |  |  |
Figura 1.
Arco del Triunfo (París).
|
Figura 2.
Monasterio de las
Huelgas (Burgos). |
Figura 3.
La Pedrera (Barcelona).
|
El problema que intenta resolver el arco es descargar el peso de la construcción cuando va a recaer sobre una zona hueca. Si no queremos que se rompa la edificación podemos diseñar una curva que haga que el peso se dirija hacia los laterales.
 |  |  |
Figura 4.
|
Figura 5.
|
Figura 6.
|
1.2 Requisitos del sistema
Esta sección usa applets de Java. Para poder visualizar e interactuar con las construcciones se necesita tener la plataforma de Java versión 6 (o superior) [http://www.java.com/es] habilitada en el ordenador.
1.3 La construcción de arcos
En el applet tenemos el diseño de un arco ojival superpuesto a la imagen de la puerta de la iglesia de San Pantaleón en Cuenca.
 |
Figura 7. Arco ojival.
|
En la parte superior hay un deslizador llamado Construcción. Si movemos el punto lentamente de izquierda a derecha veremos que el arco se borra por completo y se inicia un proceso automático en el que van apareciendo progresivamente tanto el arco como los elementos auxiliares en los que se apoya su estructura. Más adelante se realizará la propuesta de construir diez arcos distintos en la pantalla del ordenador con las orientaciones del applet y la ayuda del navegador.
Hay un segundo deslizador designado por Distancia al vértice, que permite modificar el arco ojival para poderlo ajustar a otra puerta distinta en la que la inclinación de los arcos sea diferente. En los diseños se ha tenido la previsión de dejar algún elemento móvil (normalmente uno o dos puntos) que nos permita después modificar las curvas para que se puedan ajustar a otros arcos del mismo tipo, más o menos estilizados.
1.4 La propuesta de trabajo
Hay diversos tipos de arco dependiendo de la curva que utilicemos para cerrarlo. Cada archivo contiene dos figuras: en la de la izquierda hay una imagen del arco construido y, a la derecha, otra preparada para ser diseñada por el lector. Las construcciones se han realizado con GeoGebra, tomando como fondo una imagen de ese arco utilizado en una edificación real.
 |
Figura 8. Arco de medio punto.
|
La figura de la izquierda admite animación, como ya vimos en el arco ojival: si desplazamos hacia la derecha el deslizador Construcción, vemos aparecer las indicaciones del diseño. En primer lugar desaparece el arco, y comienzan a aparecer nuevos elementos que son las pistas para la construcción geométrica de la curva.
a) El punto medio y el segmento que une ese punto con uno de los extremos.
b) El segmento comienza a girar alrededor del punto medio anterior describiendo un arco.
c) Continúa el arco.
d) El arco está completo.
e) Desaparecen los elementos accesorios para quedarnos únicamente con la curva.
 |  |  |
Figura 9a.
|
Figura 9b.
|
Figura 9c.
|
 |  |
Figura 9d.
|
Figura 9e.
|
No se pide la reproducción de ese movimiento, sólo la construcción del arco. Sobre la imagen de la derecha se puede componer la curva a partir de las herramientas de la parte superior (sólo se han seleccionado algunas de las que ofrece GeoGebra). Si se prefiere trabajar con el programa GeoGebra, previamente hay que instalarlo en el ordenador. Se descarga gratuitamente en la siguiente dirección:http://www.geogebra.org/cms. Cuando el programa está instalado, al hacer una doble pulsación sobre el applet, se abrirá el programa con el archivo que se ha creado.
En varios de los arcos hay un segundo deslizador que deja algún elemento libre para ser accionado. En el caso del arco rebajado tenemos un segundo deslizador titulado Se rebaja que indica cuánto se ha bajado el centro para que el arco no se eleve demasiado. Para verlo mejor, es interesante dejar el deslizadorConstrucción en una posición intermedia:
 |  |  |
Figura 10a.
|
Figura 10b.
|
Figura 10c.
|
 |  |
Figura 10d.
|
Figura 10e.
|
2. Arcos con GeoGebra
2.1. Arco de medio punto
El arco de medio punto utiliza media circunferencia para descargar los pesos que recaen en el espacio vacío. Comenzó a ser utilizado en Mesopotamia durante el tercer milenio a.C. y sigue siendo utilizado en la actualidad. Hemos elegido la imagen de una ventana de la iglesia de Santa Eulalia en Susín, Biescas, Huesca.
Otros ejemplos:
 |  |  |
Figura 12. Castillo de la Mola (Novelda, Alicante).
|
Figura 13. Palacio de Godoy (Cáceres).
|
Figura 14. El Partal de la Alhambra (Granada).
|
2.2. El arco rebajado
El arco rebajado se construye cuando no hay suficiente espacio en la parte superior para el arco de medio punto. La solución consiste en colocar el centro del arco más abajo que el anterior. La encontramos en la Casa Pagola en Calahorra, La Rioja.
 |
Figura 15. Casa Pagola (Calahorra, La Rioja).
|
Otros ejemplos:
 |  |
Figura 16. Puente Viejo sobre
el río Génave (Jaén).
|
Figura 17. Puente sobre el río Órbigo, Fuente
La Vizana (Alija del Infantado, León).
|
 |
Figura 18. Puerta Baja de la
muralla de Daroca (Zaragoza).
|
2.3. Arco ojival
Está compuesto por dos arcos de circunferencia simétricos. Utilizaremos una fotografía de la
iglesia de San Pantaleón en Cuenca.
 |
Figura 19. Iglesia de San Pantaleón (Cuenca).
|
Otros ejemplos:
 |  |
Figura 20. Catedral de Palencia.
|
Figura 21. Iglesia de
San Lorenzo (Ciudad Real).
|
2.4. Arco de herradura
Fue muy utilizado en el arte visigodo y en el hispano musulmán. Está compuesto por dos pequeños arcos de circunferencia a los lados y un gran arco central en la parte superior. Lo veremos en la iglesia de San Pedro de Balsemao en Lamego, Portugal.
Otros ejemplos:
 |  |
Figura 23. Mezquita de Córdoba.
|
Figura 24. Monasterio de las Claras
(Tordesillas, Valladolid).
|
2.5. El arco apuntado
Está formado por cuatro arcos de circunferencia de 60º que se colocan sobre los lados exteriores de triángulos equiláteros. Lo estudiaremos en el convento de Santo Domingo en Estella, Navarra.
 |
Figura 25. Convento de Santo Domingo(Estella, Navarra).
|
2.6. El arco conopial
Es un arco de cuatro centros que en la parte central invierte el arco hacia arriba colocando el centro en la parte superior, con ello consigue formar un vértice. Lo veremos sobre una imagen de la Cartuja de Sevilla.
 |
Figura 26. La Cartuja de Sevilla.
|
Otros ejemplos:
 |  |
Figura 27.
Catedral de Murcia.
|
Figura 28. Iglesia de Santa María Magdalena
(Torrelaguna, Madrid).
|
2.7. El arco carpanel
El arco carpanel es un arco rebajado con tres centros; dos de ellos se utilizan para formar pequeños arcos en los extremos, por lo que adquiere una forma redondeada. Lo vamos a estudiar en la portada de una casa de Palma de Mallorca.
 |
Figura 29. Casa en Palma de Mallorca.
|
Otros ejemplos:
 |  |  |
Figura 30. Cáceres.
|
Figura 31. Hospital de Nuestra Señora de los Milagros (Guadalcanal, Badajoz).
|
Figura 32. Puerta de Loreto (Orihuela, Alicante).
|
2.8. El arco trebolado
Está formado por tres arcos de circunferencia que reproducen el perfil de un trébol. Lo tenemos en elMihrab de la Mezquita de Córdoba.
 |
Figura 33. Mihrab de la Mezquita de Córdoba.
|
Otros ejemplos:
 |  |
Figura 34. Catedral de
Santiago de Compostela.
|
Figura 35. Mezquita de Córdoba.
|
2.9. El arco tudor
Es un arco rebajado que se construye a partir de cuatro centros: dos de ellos, de radio más pequeño, sirven para redondear los extremos, mientras que los otros dos tienen el centro en la parte inferior y se unen en la mediatriz. Se ha construido sobre una imagen de una de las puertas del Taj Mahal en la India.
 |
Figura 36. Puerta del Taj Mahal (India).
|
Otros ejemplos:
 |  |
Figura 37. Mezquita del Imam (Isfahan, Irán).
|
Figura 38. Puente Khaju (Isfahan, Irán).
|
 |
Figura 39. Taj Mahal (Agra, India).
|
2.10. El arco rampante
Es asimétrico y está formado por dos arcos de 90º, uno con mayor radio que el otro, mientras que la suma de los dos radios es igual al segmento AB. Lo encontramos en las puertas traseras de la iglesia de la Magdalena junto al castillo de la Mola en Novelda, Alicante.
Sobre los autores
| |
El equipo G4D [http://geometriadinamica.es] está formado por José Manuel Arranz, Rafael Losada, José Antonio Moray Manuel Sada. Miembros del equipo Intergeo para la difusión de la geometría dinámica y del Instituto GeoGebra de Cantabria, coordinan la sección Geometría Dinámica y Matemáticas Interactivas del portal DivulgaMAT.
| |
 |
José Manuel Arranz San José [http://roble.pntic.mec.es/jarran2] es profesor de Matemáticas del IES Europa de Ponferrada (León), profesor asociado de Matemáticas de la Universidad de León y autor de las webs Geometría Dinámica-Cabri II y Geometría Activa, que ha recibido varios premios. Ha sido asesor de Matemáticas del Centro de Profesores de Ponferrada y miembro del consejo asesor de la revista SUMA.
|
 |
Rafael Losada Liste [http://www.iespravia.com/rafa/rafa.htm] es profesor de Matemáticas en el IES de Pravia (Asturias). Autor de La Programación de Matemáticas con Recursos Interactivos, coordina la sección de Música y Matemáticas de DivulgaMAT. Está certificado por el International GeoGebra Institute como GeoGebra Institute Trainer asociado al Instituto GeoGebra de Cantabria.
|
 |
José Antonio Mora Sánchez [http://jmora7.com] es profesor de Matemáticas en el IES Sant Blai de Alicante. Ha sido asesor para la Reforma del Sistema Educativo en la Comunidad Valenciana (1985-88) y asesor de Matemáticas del Centro de Profesores de Alicante (1990-95). Miembro del equipo T3, dedicado a la introducción de las NNTT en la enseñanza de las matemáticas, pertenece al comité asesor de la revista UNO y al consejo de redacción de la revista SUMA.
|
 |
Manuel Sada Allo [http://recursos.pnte.cfnavarra.es/~msadaall/geogebra/ index.htm] es profesor de Matemáticas del IES Zizur. Actualmente trabaja como asesor de Matemáticas del Centro de Apoyo al Profesorado de Pamplona (Navarra). Es autor de las webs Recursos informáticos y audiovisuales para el aula de Matemáticas y Ejemplos diversos de webs interactivas de Matemáticas con GeoGebra.
TOMADO DE: http://www.matematicalia.net/index.php?option=com_content&task=view&id=448&Itemid=272 |
Suscribirse a:
Entradas (Atom)
Archivo del blog
-
►
2017
(19)
- ► septiembre (1)
-
▼
2014
(441)
- ► septiembre (61)
-
►
2011
(38)
- ► septiembre (4)
-
►
2010
(74)
- ► septiembre (6)



