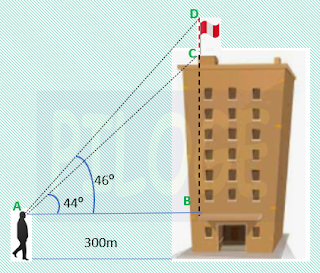
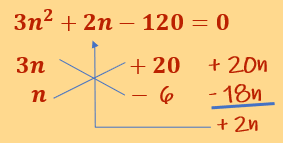Una caja tiene un volumen de 80〖𝑐𝑚〗^3. Si se abre por las esquinas como se muestra en la figura, se puede determinar que está hecha de un cuadrado de latón recortado cada esquina en forma de un cuadrado de 3 cm de lado. Determina las dimensiones originales de la caja.
SOLUCIÓN
El Volumen es el producto de las 3 dimensiones: